Max Planck was born in Kiel, Germany, in 1858. He came from a family of distinguished scholars, his father being a professor of law at the University of Kiel. Planck showed an early aptitude for mathematics and physics. He studied at the University of Munich, where he was taught by some of the leading physicists of the day such as Hermann von Helmholtz and Gustav Kirchhoff.
After graduating from Munich, Max Planck continued his studies at the University of Berlin, where he worked with Heinrich Hertz, who had recently discovered electromagnetic waves. In 1885, Planck completed his doctorate, and he then took a position as a professor at the University of Kiel.
Planck’s early work focused on theoretical physics, and he made significant contributions to the understanding of thermodynamics and statistical mechanics. However, it was his work on blackbody radiation that would ultimately change the course of physics. By introducing the concept of quantization, Planck’s work not only accurately explained blackbody radiation but also established the foundation of modern quantum mechanics. This innovative step, taken with mathematical precision and unwavering dedication, earned Planck the Nobel Prize in Physics in 1918.
As we delve into Planck’s groundbreaking work, it is essential to comprehend the scientific landscape he inherited.
The Existing Theory and Formula: The Classical Dilemma
In the early 20th century, classical physics encountered a perplexing dilemma: it failed to explain the observed behaviour of blackbody radiation. This baffling phenomenon, where objects emit and absorb radiation based on their temperature, could not be elucidated using classical theories. As temperatures rose, classical physics predicted an infinite amount of emitted radiation, leading to the notorious “ultraviolet catastrophe“.
The theories put forth by luminaries like Lord Rayleigh and Wilhelm Wien were rooted in classical electromagnetism and statistical mechanics.
Lord Rayleigh’s equation is a classical theory of blackbody radiation that was developed in 1900. The equation is based on the assumption that the oscillating electric fields within a blackbody cavity are independent of each other.
E = kλ^4where:
- E: is the energy radiated by the oscillators
- k: is a constant
- λ: is the wavelength of the radiation
Rayleigh’s law was a significant improvement over previous theories of blackbody radiation, but it still had one major flaw: it predicted that the energy radiated by the oscillators would increase without bound as the frequency approached the ultraviolet region. This prediction was in direct contradiction to experimental data, which showed that the energy radiated by blackbodies actually decreased at high frequencies.

On the other hand, Wilhelm Wien’s displacement law provided a mathematical relationship between the wavelength of peak blackbody radiation and temperature. While his law worked well for higher frequencies, it failed miserably at lower frequencies, again diverging from experimental evidence.
Wien’s equation is given by the following formula:
λ_max T = bwhere:
- λ_max: Represents the wavelength of electromagnetic radiation at which the spectral radiance of a blackbody is maximum. It is the peak wavelength of the blackbody radiation spectrum.
- T: Denotes the temperature of the blackbody in Kelvin. The formula shows that the product of peak wavelength and temperature remains constant for a given blackbody.
- b: Is Wien’s displacement constant, a universal constant with a value of approximately 2.898 x 10^-3 m·K. It relates the temperature of a blackbody to the wavelength at which the peak of its emission occurs.
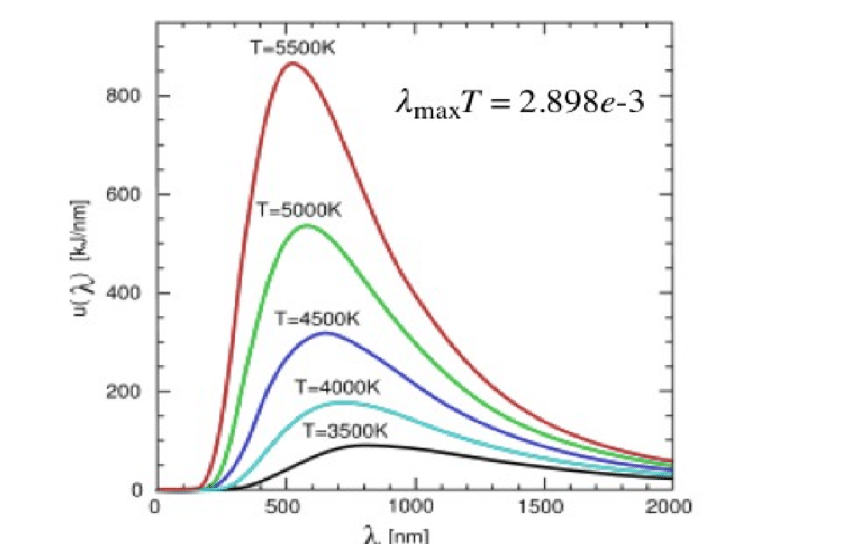
Wien’s displacement law was a significant improvement over previous theories of blackbody radiation. However, it did not work well for lower frequencies. This is because classical electromagnetism predicts that the energy of a photon is proportional to its frequency. However, quantum mechanics tells us that the energy of a photon is proportional to its frequency multiplied by Planck’s constant.
These theories, though valiant attempts, fell short of explaining the distribution of energy in the blackbody spectrum accurately. They ultimately succumbed to the ultraviolet catastrophe, revealing the limitations of classical physics in describing the behavior of electromagnetic radiation at small scales.
Therefore, Max Planck, an astute theoretician, recognized the gravity of the situation. Determined to reconcile theory with observation, he embarked on a revolutionary journey. In 1900, he presented a paper proposing a radical solution: the concept of energy quantization.
Max Planck Contribution: The Birth of Quantum Theory
It was Max Planck, with his revolutionary quantum hypothesis, who successfully bridged the gap and offered an elegant solution to the ultraviolet catastrophe by proposing the following equation:
B(λ, T) = (2hc² / λ⁵) * (1 / (e(hc / λkBT) - 1))where:
- B(λ,T): represents the spectral radiance of a blackbody at a specific wavelength (λ) and temperature (T). Spectral radiance measures the amount of electromagnetic radiation (light) emitted or reflected by an object at a particular wavelength.
- h: is Planck’s constant, which is a fundamental constant of nature. Its value is approximately 6.626 x 10^-34 Joule-seconds (J·s).
- c: represents the speed of light in a vacuum.
- λ: denotes the wavelength of electromagnetic radiation. Wavelength is the distance between consecutive crests or troughs of a wave. It is usually measured in meters (m) or other units of length.
- kB: is the Boltzmann constant, another fundamental constant of nature. Its value is approximately 1.380649×10^−23 Joules per Kelvin (J/K). The Boltzmann constant is essential in statistical mechanics and connects the average kinetic energy of particles in a system to its temperature.
- T: represents the temperature of the blackbody in Kelvin (K). Temperature determines the average thermal energy of particles within the blackbody and influences the amount and distribution of radiation emitted.
At the heart of Planck’s quantum theory lies the concept of quantization, where energy is confined to specific, quantized levels rather than a continuous spectrum. Max Planck suggested that electromagnetic energy could only be emitted or absorbed in discrete units, or “quanta,” rather than a continuous spectrum. Planck’s formula mathematically represented the energy quanta as the product of the frequency of the radiation and a constant now known as Planck’s constant (h).
This insight shattered classical physics’ assumption of smooth energy transitions and introduced a new paradigm for understanding the behaviour of atoms and molecules.
The Concept of Quantization
The concept of quantization was not new to physics when Max Planck proposed his equation. In 1900, Einstein had already proposed that light was emitted and absorbed in discrete units, which he called “quanta.” However, Planck’s equation was the first to provide a quantitative description of the quantization of energy.
In quantum mechanics, the energy levels of electrons in atoms are quantized and described by the Schrödinger equation. The Schrödinger equation is a partial differential equation that relates the wave function of a particle to its energy. The wave function is a mathematical function that describes the probability of finding the particle at a particular location. The Schrödinger equation can be used to calculate the energy levels of electrons in atoms, as well as the wave functions of other particles.
The time-dependent Schrödinger equation for a single non-relativistic particle is given by:
Ψ(x, t) = (ħ² / 2m) ∇² Ψ(x, t) + V(x, t) Ψ(x, t)where:
- Ψ(x, t): is the wave function of the particle, which is a mathematical function that represents the probability amplitude of finding the particle at position “x” at time “t.”
- ħ: (h-bar) is the reduced Planck constant, which is equal to the Planck constant “h” divided by 2π (ħ = h / 2π). It appears in the equation due to the wave-particle duality of quantum mechanics.
- ∇^2: is the Laplacian operator, representing the sum of the second partial derivatives of the wave function with respect to the spatial coordinates (x, y, z, etc.). It describes the kinetic energy of the particle.
- V(x, t): is the potential energy function of the particle, which depends on both position “x” and time “t.” It represents the potential energy experienced by the particle in the given spatial and temporal context.
In the case of the hydrogen atom, the following equation can be derived from the Schrödinger equation.
E_n = -(13.6 eV) / (n^2)where:
- En: represents the energy level of the electron,
- n: is the principal quantum number (an integer representing the energy level), and
- 13.6 eV is the ionization energy of hydrogen.
The value of the energy level depends on the principal quantum number, n which can take any integer value from 1 to infinity. The lower the value of n the lower the energy level.
In the case of n = 1, the energy of the electron in this level is -13.6 eV.
Real Stories of Quantum Revolution: Max Planck Legacy Lives On
Numerous empirical studies have confirmed the astonishing behavior of particles at the quantum level, showcasing phenomena such as superposition, entanglement, and wave-particle duality. For instance, the famous double-slit experiment revealed that particles, like electrons, can exist in multiple states simultaneously, demonstrating their wave-like nature. This experiment has been replicated countless times, providing irrefutable evidence of the validity of quantum theory.
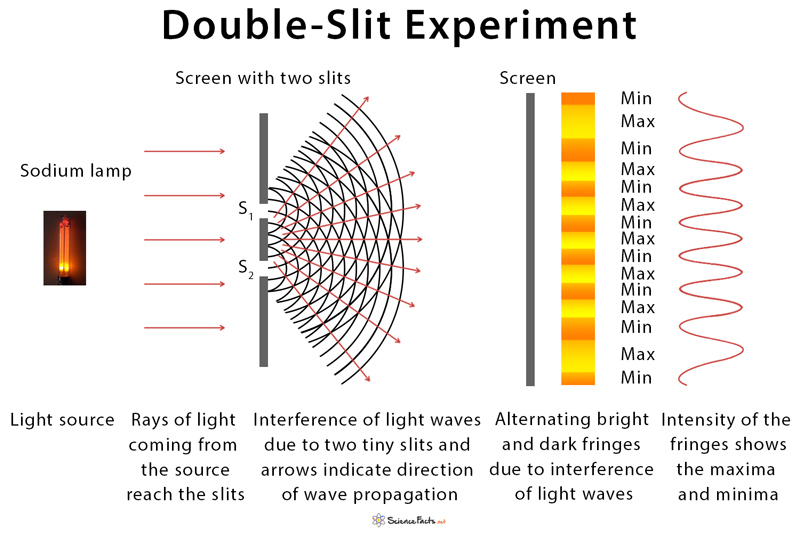
Furthermore, the groundbreaking discovery of quantum teleportation, where quantum information is transferred instantaneously over large distances, has pushed the boundaries of our understanding of entanglement. Experiments conducted with entangled particles have demonstrated correlations that defy classical explanations and firmly support the principles of quantum mechanics.
In addition to empirical evidence, prominent modern physicists have spoken about Max Planck’s profound legacy in quantum physics. Nobel laureate Richard Feynman once said,
“I think I can safely say that nobody understands quantum mechanics.”
This quote reflects the complexity and mysterious nature of quantum theory that Planck’s initial work set in motion.
Indeed, Planck’s revolutionary insights have inspired generations of physicists, with Steven Weinberg, another Nobel laureate, remarking,
“Every theoretical physicist who is any good knows six or seven different theoretical representations for exactly the same physics.”
This highlights the versatility of quantum theory in describing the natural world.
Conclusion
Max Planck’s work laid the groundwork for modern quantum physics, and his contributions continue to shape scientific advancements today.
Share this fascinating journey with others and contribute your thoughts in the comments, as we celebrate the genius of Planck and the timeless legacy of quantum physics. Don’t forget to invite fellow enthusiasts to join the discussion!
References
- Nouredine Zettili, “Quantum Mechanics: Concepts and Applications,” 2nd ed., Wiley, 2009.
- David J. Griffiths, “Introduction to Quantum Mechanics,” 2nd ed., Cambridge University Press, 2016.
- Niels Bohr, “On the Constitution of Atoms and Molecules,” Philosophical Magazine, Vol. 26, No. 151, 1913, pp. 1-25.








