Journey into the Enigmatic World of Black Holes

It is truly remarkable how a phenomenon we’ve been familiar with since childhood – gravitational attraction – lies at the core of the Big Bang, the evolution of the universe, black holes, gravitational waves, and some of the most profound unanswered inquiries in fundamental physics.

But before we dive into these mysteries, let’s take a step back in time.

According to Aristotle, the movement of objects stemmed from their inherent inclination to seek their “natural” place. However, Galileo Galilei’s groundbreaking research challenged this notion, revealing that an object’s resistance to changes in motion or rest is governed by its characteristic feature, now known as “inertial mass.”

A generation later, Isaac Newton formalized these concepts in his theory of mechanics, according to which inertial mass is the constant of proportionality between the “force” acting on a body and its acceleration. Newton went further and identified in the “gravitational force” the cause of the Earth’s attraction on all bodies, from the famous apple (which, according to a legend, would have fallen on his head) to the Moon, as well as the universal mutual attraction between all celestial bodies.

According to Newton, any two objects attract each other proportionally to their masses (what we now call “gravitational masses”) and inversely proportional to the square of their distance.

It was a revolution.

When linked with mechanics, this simple theory provides an extraordinarily perfect description of all gravitational phenomena: the motion of the Moon around the Earth, eclipses, tides, Kepler’s laws for the solar system, and the motion of projectiles or satellites. However, Newton’s theory of gravitation had two key unresolved problems.

One was obvious from the start: as Galileo’s famous experiments from the leaning tower demonstrated, the “inertial” and “gravitational” masses are identical from an experimental perspective. Why are two seemingly unrelated concepts (inertia and gravity) linked to each other?

The second problem was raised later by Albert Einstein in his annus mirabilis (1905), when he formulated the theory of special relativity, which claims that the speed of light in a vacuum is constant and that it is the maximum speed possible in nature.

Special relativity was promptly confirmed by different experiments, although it was in stark contrast to Newton’s theory, in which the gravitational interaction propagates at unlimited speed (and not at the speed of light).

Einstein’s solution

Einstein approached these two unresolved problems with utmost seriousness, recognizing their significance despite being considered somewhat peripheral at the time. He embarked on a decade-long journey of rigorous study, which ultimately culminated in his magnum opus: the theory of general relativity.

General relativity, like many of Einstein’s remarkable contributions, is built upon a foundation of principles and theoretical axioms grounded in empirical observations. In his quest to reconcile the challenges posed by Newton’s theory, Einstein proposed a fundamental principle: the invariance of physical laws regardless of the observer’s motion. This meant that the laws of nature should hold true in any reference frame.

Moreover, drawing upon Galileo’s seminal observations, Einstein formulated the “equivalence principle.” This principle posits that inertial mass and gravitational mass, which may appear distinct, are actually one and the same physical quantity. In other words, the effects of gravity on an object are indistinguishable from those experienced in an accelerated reference frame.

These fundamental concepts have highly astonishing consequences, such as the fact that it is hard to locally discern whether a system is subject to gravitational attraction or accelerated motion.

In his famous elevator experiment, Einstein demonstrated that, for an observer inside an elevator accelerating in a vacuum, objects fall as if subjected to the earth’s gravitational force in a stationary elevator. The two situations are indistinguishable.

Similarly, it is impossible to tell the difference between the elevator in free fall in the earth’s gravitational field and the elevator at rest in empty space.

The rationale demonstrates that gravitational attraction can be locally abolished in an appropriate reference system due to the equality of gravitational mass and inertial mass. This simple concept represents the foundation of the general relativity theory.

Einstein spent the next few years looking for a suitable mathematical formalism for his theory and found it in differential geometry. His remarkable idea was to define gravitational interaction as a purely geometric effect: the fact that gravity can be removed locally is similar to the well-known fact that the Earth appears flat to us on small scales, although spherical.

Einstein identified the “curvature of spacetime” as the fundamental physical quantity to describe gravity.

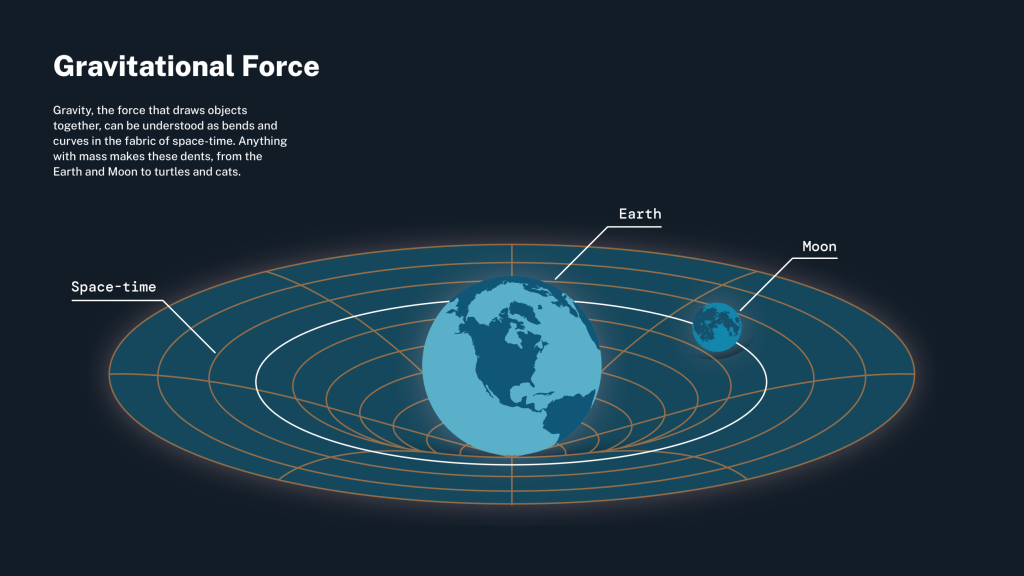
Locally, spacetime is flat and the laws of special relativity apply, but globally spacetime is curved and dynamic: it can twist, and deform.

The source of this distortion is the energy (to be precise, what is technically called “energy-impulse tensor”) of the system, in all its forms, including kinetic energy. One of the forefathers of general relativity as a modern subject of study, physicist John Archibald Wheeler, summed up the question succinctly with a slogan:

“Spacetime tells matter how to move, matter tells spacetime how to bend.”

The advent of the revolutionary theory of general relativity presented a considerable challenge for even the most brilliant minds of Einstein’s era. Certain phenomena predicted by this new theory, which would have been inexplicable within the framework of Newtonian mechanics, garnered significant interest as potential confirmations of Einstein’s concepts. One of the most renowned examples is the deflection of light.

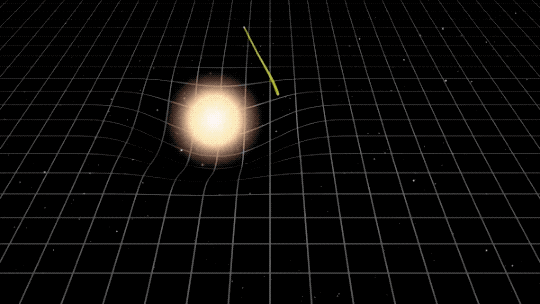
If gravity is indeed the result of motion within a curved spacetime, then this curvature should impact all objects, including light itself. Consequently, the light would be compelled to follow a curved trajectory and deviate from a straight path when in the presence of massive masses or significant concentrations of energy. This unimaginable event was noticed by Arthur Eddington during the historic 1919 eclipse, and it contributed to the popular perception of Einstein as a global scientific “star.”

Einstein’s theory also predicted small variations with respect to Keplerian orbits in the solar system; in particular, he was able to explain a small discrepancy in the advancement of Mercury’s perihelion that had tormented astronomers for decades.

Finally, he anticipated that the frequency of radiation emitted by a star was higher near the star than far away (the so-called “gravitational redshift”). This phenomenon, which has also been experimentally confirmed, is related to the fact that time moves more slowly near large masses. This is a critical component for the operation of GPS, which must account for the influence of the Earth’s gravitational field on signals sent to satellites for geolocation.

Applications of General Relativity

Despite being remarkable, the effects outlined by general relativity are negligible in our daily life.

Newtonian gravity remains a good approximation since the curvature caused by a star like the Sun is little and the solar system’s spacetime on Earth can be therefore considered almost flat. However, there are situations in which the curvature of spacetime can be extreme: in that case, general relativity becomes essential.

Its first application is in cosmology. The origin of the universe was a philosophical (and theological) topic prior to Einstein. However, in the perspective of general relativity, the cosmos as a whole can be represented as spacetime evolving in relation to matter (visible and invisible) and radiation, starting with an initial configuration of extremely high spacetime density and curvature (the Big Bang).

Another instance in which general relativity is important is the study of large stars.

If the Sun affects spacetime only a little, what if all of its mass was compacted into a much smaller and denser star? The curvature of spacetime would be substantially higher in such a situation, and phenomena like light deflection and gravitational dilation of time would be greatly exacerbated.

For example, light could be deflected to the point where it becomes imprisoned in the star’s gravitational field. A star of this type could not produce any radiation and would appear in the sky as a “black hole.”

Furthermore, because the speed of light is the fastest possible in nature, anything that enters this black hole (crossing the event horizon) would be swallowed up forever and would be unable to communicate with the outside world.

But how can an object that by definition absorbs everything, including light, be “observed”? In addition to the study of orbits (as in the case of Sagittarius A *) or of the hot matter falling into them (as in the case of the photo of M87), the possibility of “seeing” black holes is provided by a further astonishing prediction of Einstein: gravitational waves.

Gravitational Waves

These spacetime ripples are produced by huge moving masses in the same way that a speedboat produces waves in the sea or accelerated electrical charges produce electromagnetic waves, and they propagate at the speed of light.

Gravitational waves are produced by any mass in accelerated motion, although they are usually too weak to be detected. The cosmic collision of two black holes, on the other hand, generates massive power (about one billion million times the power of the Sun), and the resulting gravitational waves propagate unaffected for billions of light years.

The Ligo-Virgo collaboration detected the first gravitational wave created by the merger of two black holes on September 14, 2015, and named it GW150914 (which stands for “gravitational wave” of 09/14/15). This monumental event heralded the start of a new astronomy that is still in its early stages.

All of these observations are pushing uncharted territory and have the potential to transform entire fields of astrophysics, cosmology, and fundamental physics.

Future investigations, like the third-generation Einstein Telescope interferometer, the Lisa space mission, and precise radiopulsar measurements, will allow for the detection of gravitational waves in previously unseen frequency ranges. In addition to gaining a better understanding of the cosmos, it is hoped that these observations will lead to the discovery of new unexpected signals, potentially providing light on certain unanswered questions about gravity. One of the most crucial unanswered questions is what happens inside a black hole.

Life Inside Black Holes

Several theorems, demonstrated by the notable physicists Stephen Hawking and Roger Penrose (who were awarded the 2020 Nobel Prize in Physics for their groundbreaking work), have shed light on the existence of a “singularity” within a black hole. This singularity represents a region in spacetime where curvature becomes infinite and Einstein’s theory of gravity no longer applies.

The nature of what occurs near the singularity remains veiled by the presence of the event horizon, making it inaccessible for direct observation from the outside. Nonetheless, it is anticipated that as the curvature surrounding the singularity approaches the Planck scale, the quantum effects of gravity will assume significance and fundamentally alter our understanding of general relativity.

The quest for a quantum theory of gravity, which seeks to resolve the conundrum of singularities, stands as the “Holy Grail” of modern theoretical physics. Two prominent theoretical proposals, namely loop quantum gravity and string theory, take contrasting approaches in incorporating quantum effects into Einstein’s theory.

Ultimately, only future experimental observations, yet to be made, hold the key to unravelling these mysteries. Once again, it is conceivable that the solution to these intricate puzzles may stem from revisiting the age-old question:

What precisely causes objects to fall?